Survival Distributions with piece-wise constant hazards and multiple states
Source:R/multistate.R
dmstate.RdDensitiy, distribution function, hazard function, cumulative hazard function and survival function of multi-state survival functions.
Usage
dmstate(x, t, Q, pi, abs)
pmstate(q, t, Q, pi, abs)
hmstate(x, t, Q, pi, abs)
chmstate(x, t, Q, pi, abs)
smstate(q, t, Q, pi, abs)Value
dmstate gives the density evaluated at x.
pmstate gives the distribution function evaluated at q.
hmstate gives the hazard function evaluated at x.
chmstate gives the cumulative hazard function evaluated at x.
smstate gives the survival function evaluated at q.
Details
Q is an array of dimensions N x N x M where M is the number of time intervals
and N is the number of states. Every slice of Q along the third dimension is
an N x N Q-matrix. Each row of the Q-matrix contains the hazard-rates for
transitioning from the respective state to each other state in the
off-diagonal elements. The diagonal element is minus the sum of the other
elements (such that the row sums are 0 for each row). (See Norris (1997) Part
2, Continuous-time Markov chains I, for the definition of Q-matrices and the
theory of continuous time markov chains.)
abs is a vector that is one for each absorbing state that corresponds to an
event of interest and zero everywhere else. With this different events of
interest can be encoded for the same model. For example overall survival and
progression free survival can be encoded by setting abs to one in the
"death" state or the "death" and the "progressed disease" state and leaving
Q and pi the same.
The initial distribution pi can be used to set the probabilities of
starting in different stages. The starting distribution in combination with
Q can be used to model sub-populations. The corresponding values of pi
are then the prevalence of the sub-populations in the initial state.
The densities, distribution functions, ... now correspond to the event of
entering one of the absorbing states when the initial distribution in the
states is pi.
Functions
dmstate(): density of survival distributions for a piece-wise exponential multi-state modelpmstate(): distribution function of survival distributions for a piece-wise exponential multi-state modelhmstate(): hazard of survival distributions for a piece-wise exponential multi-state modelchmstate(): cumulative hazard of survival distributions for a piece-wise exponential multi-state modelsmstate(): survival function of survival distributions for a piece-wise exponential multi-state model
Examples
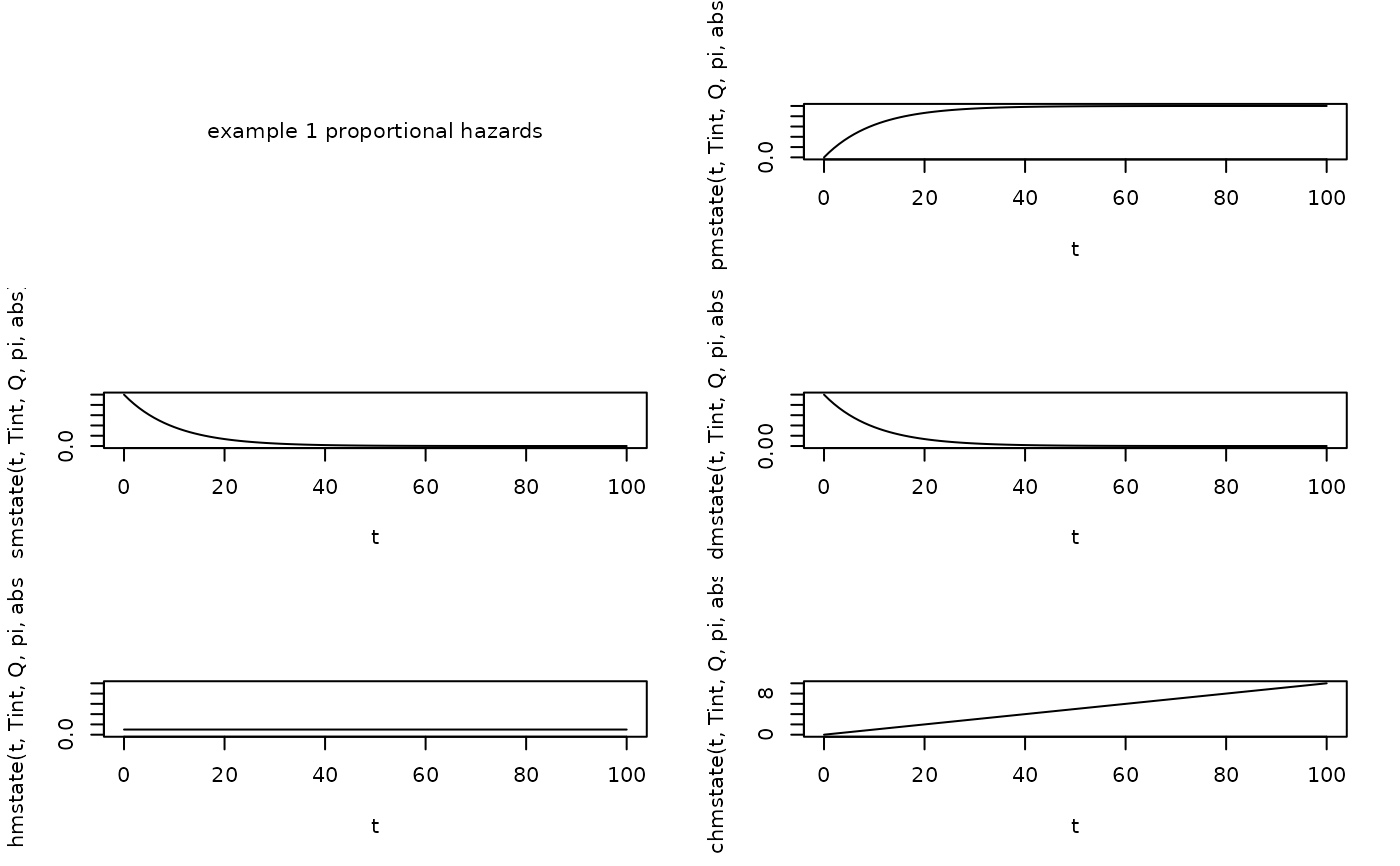
# Example 1: Proportional Hazards
Tint <- 0
Q <- matrix(
c(
-0.1, 0.1,
0 , 0
), 2, 2, byrow = TRUE
)
dim(Q) <- c(2,2,1)
pi <- c(1,0)
abs <- c(0,1)
t <- 0:100
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 1 proportional hazards")
plot(t, pmstate(t, Tint, Q, pi, abs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs), type="l")
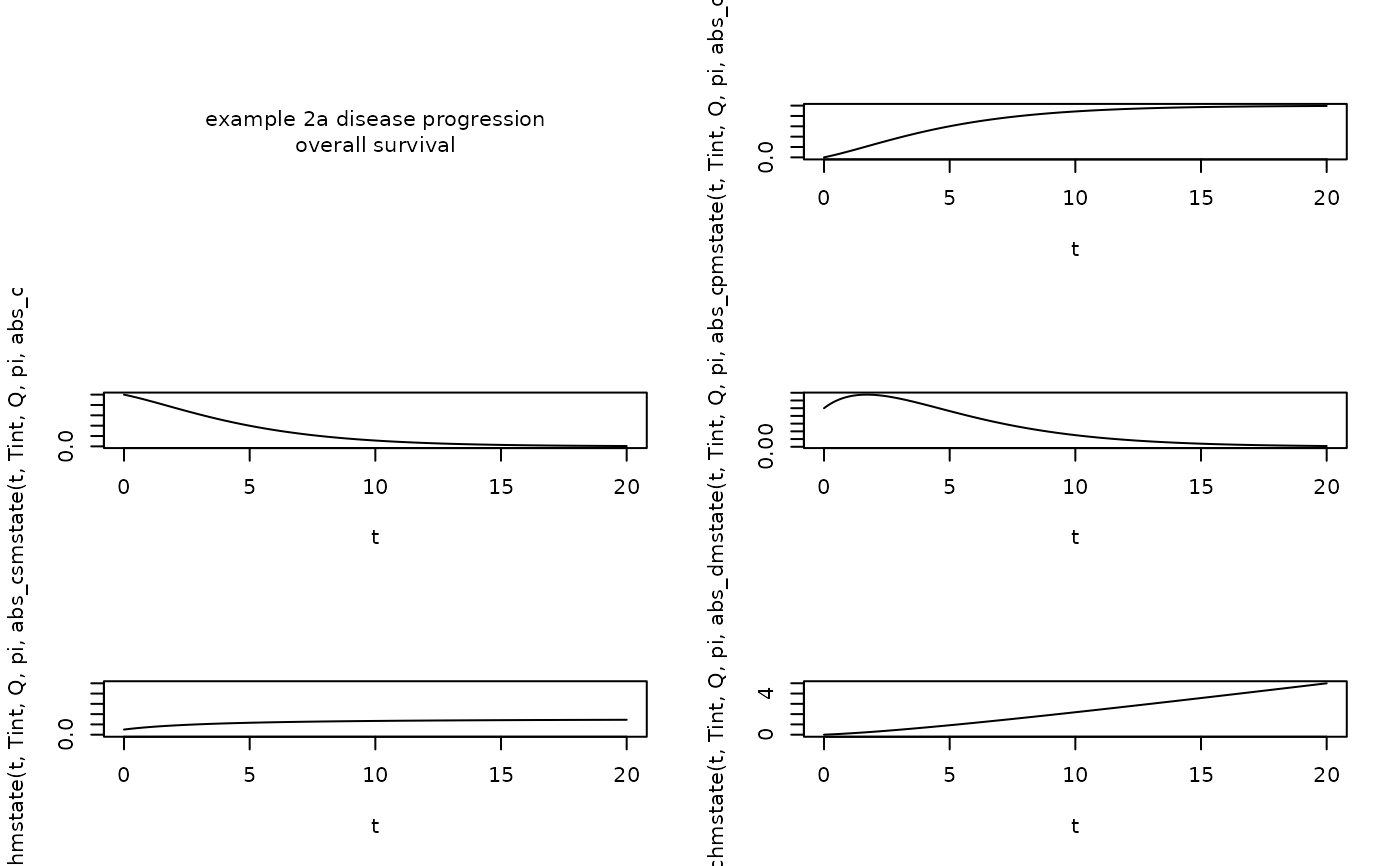
 # Example 2: Disease Progression
Tint <- 0
Q <- matrix(
c(
-0.3, 0.2, 0.1,
0 ,-0.4, 0.4,
0 , 0, 0
), 3, 3, byrow = TRUE
)
dim(Q) <- c(3,3,1)
pi <- c(1,0,0)
abs_os <- c(0,0,1)
abs_pfs <- c(0,1,1)
t <- seq(0,20, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 2a disease progression\noverall survival")
plot(t, pmstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, smstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs_os), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs_os), type="l")
# Example 2: Disease Progression
Tint <- 0
Q <- matrix(
c(
-0.3, 0.2, 0.1,
0 ,-0.4, 0.4,
0 , 0, 0
), 3, 3, byrow = TRUE
)
dim(Q) <- c(3,3,1)
pi <- c(1,0,0)
abs_os <- c(0,0,1)
abs_pfs <- c(0,1,1)
t <- seq(0,20, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 2a disease progression\noverall survival")
plot(t, pmstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, smstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs_os), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs_os), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs_os), type="l")
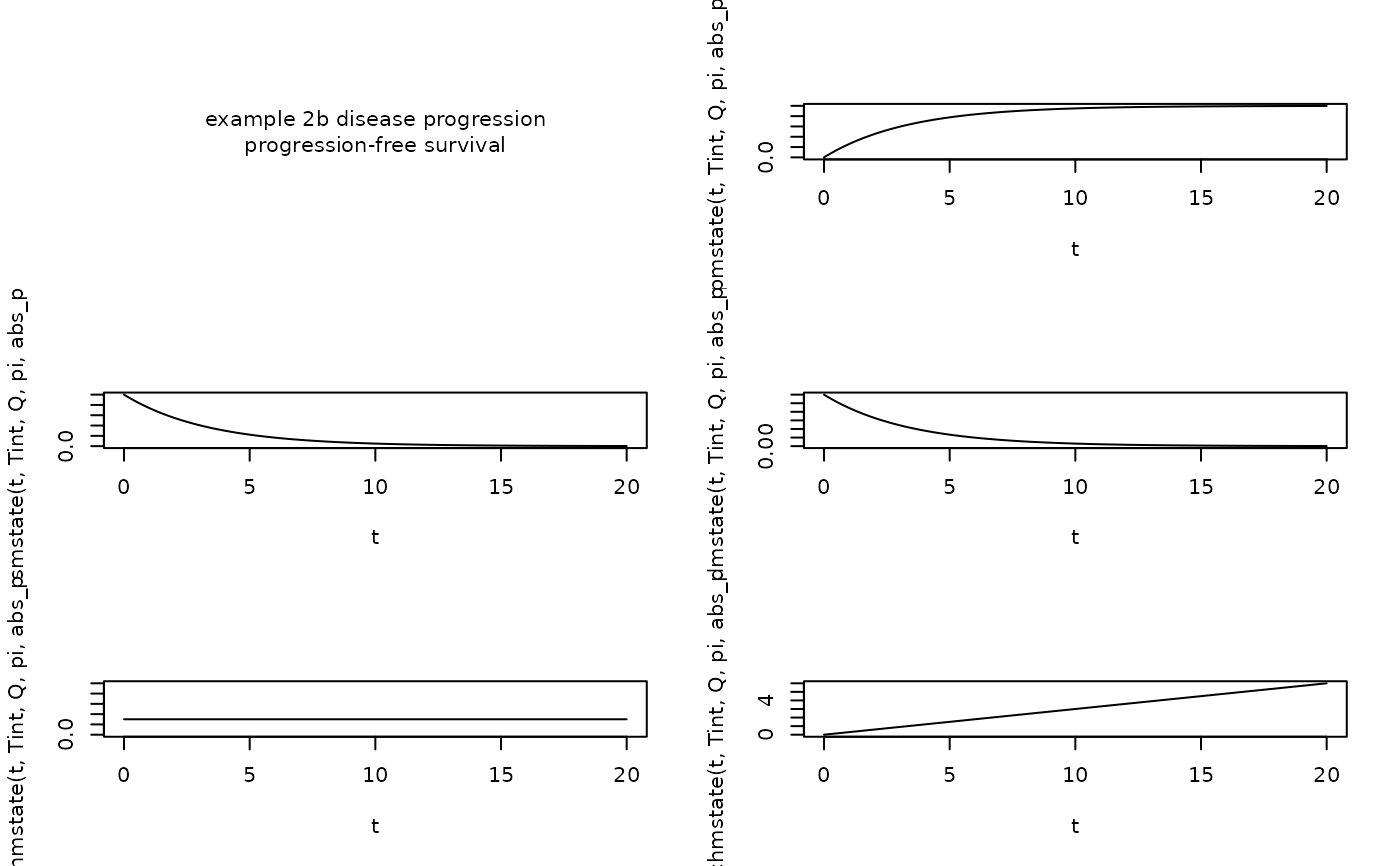
 par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 2b disease progression\nprogression-free survival")
plot(t, pmstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs_pfs), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs_pfs), type="l")
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 2b disease progression\nprogression-free survival")
plot(t, pmstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs_pfs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs_pfs), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs_pfs), type="l")
 # Example 3: Sub-Populations
Tint <- 0
Q <- matrix(
c(
-0.4, 0 , 0.4,
0 ,-0.1, 0.1,
0 , 0, 0
), 3, 3, byrow = TRUE
)
dim(Q) <- c(3,3,1)
pi <- c(0.5,0.5,0)
abs <- c(0,0,1)
t <- seq(0, 40, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 3 sub-populations")
plot(t, pmstate(t, Tint, Q, pi, abs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs), type="l")
# Example 3: Sub-Populations
Tint <- 0
Q <- matrix(
c(
-0.4, 0 , 0.4,
0 ,-0.1, 0.1,
0 , 0, 0
), 3, 3, byrow = TRUE
)
dim(Q) <- c(3,3,1)
pi <- c(0.5,0.5,0)
abs <- c(0,0,1)
t <- seq(0, 40, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 3 sub-populations")
plot(t, pmstate(t, Tint, Q, pi, abs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs), type="l", ylim=c(0,1))
plot(t, chmstate(t, Tint, Q, pi, abs), type="l")
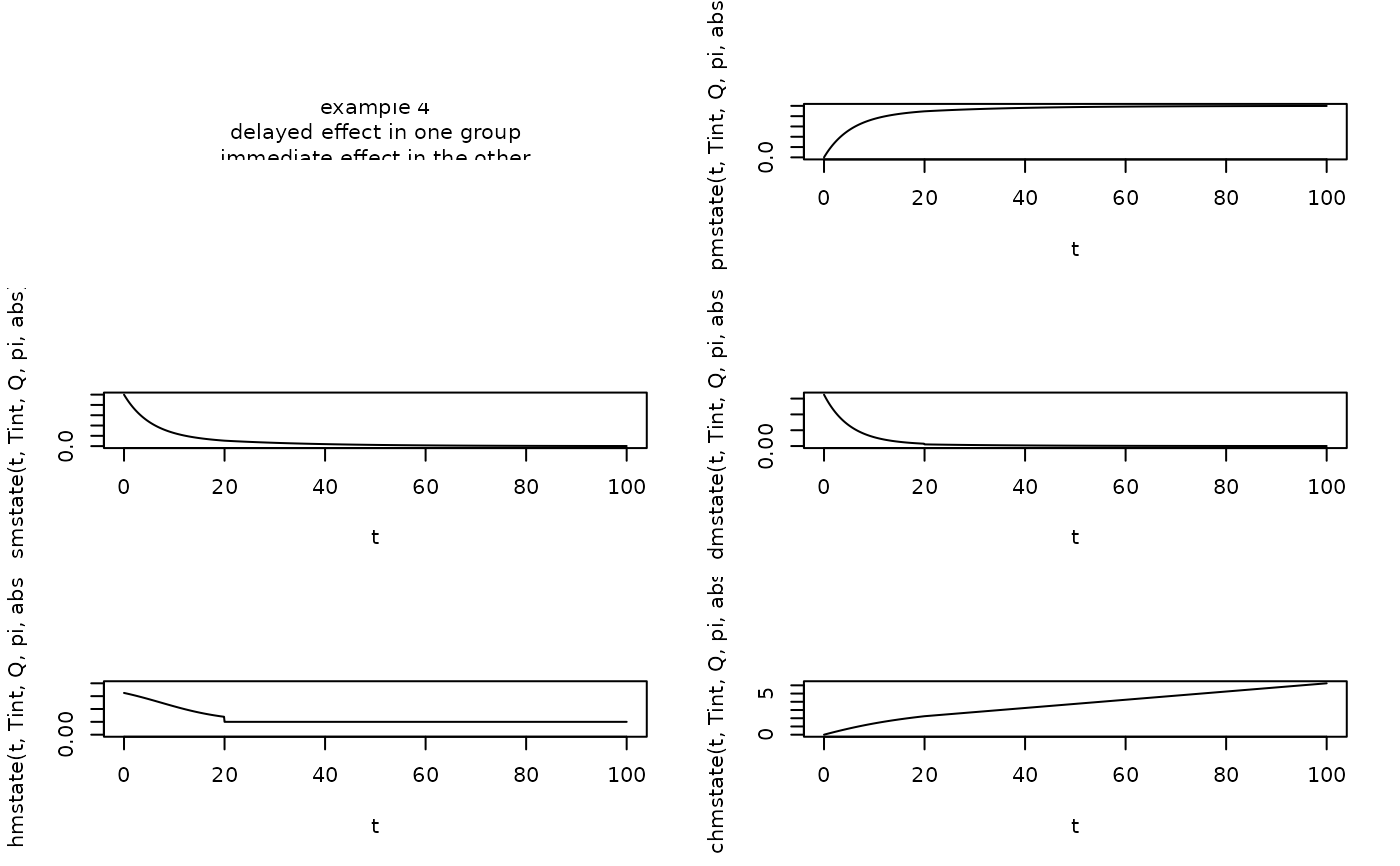
 # Example 4: Delayed Effect in one group and immediate effect in the other group
Tint <- c(0,20)
Q <- array(NA_real_, dim=c(3,3,2))
Q[,,1] <- matrix(
c(
-0.2, 0 , 0.2 ,
0 ,-0.05, 0.05,
0 , 0, 0
), 3, 3, byrow = TRUE
)
Q[,,2] <- matrix(
c(
-0.05, 0 , 0.05 ,
0 ,-0.05, 0.05,
0 , 0, 0
), 3, 3, byrow = TRUE
)
pi <- c(0.75,0.25,0)
abs <- c(0,0,1)
t <- seq(0, 100, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 4\ndelayed effect in one group\nimmediate effect in the other")
plot(t, pmstate(t, Tint, Q, pi, abs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs), type="l", ylim=c(0,0.2))
plot(t, chmstate(t, Tint, Q, pi, abs), type="l")
# Example 4: Delayed Effect in one group and immediate effect in the other group
Tint <- c(0,20)
Q <- array(NA_real_, dim=c(3,3,2))
Q[,,1] <- matrix(
c(
-0.2, 0 , 0.2 ,
0 ,-0.05, 0.05,
0 , 0, 0
), 3, 3, byrow = TRUE
)
Q[,,2] <- matrix(
c(
-0.05, 0 , 0.05 ,
0 ,-0.05, 0.05,
0 , 0, 0
), 3, 3, byrow = TRUE
)
pi <- c(0.75,0.25,0)
abs <- c(0,0,1)
t <- seq(0, 100, by=0.1)
par(mfrow=c(3,2))
plot.new()
text(0.5,0.5,"example 4\ndelayed effect in one group\nimmediate effect in the other")
plot(t, pmstate(t, Tint, Q, pi, abs), type="l")
plot(t, smstate(t, Tint, Q, pi, abs), type="l")
plot(t, dmstate(t, Tint, Q, pi, abs), type="l")
plot(t, hmstate(t, Tint, Q, pi, abs), type="l", ylim=c(0,0.2))
plot(t, chmstate(t, Tint, Q, pi, abs), type="l")